Hasse norm theorem

In number theory, the Hasse norm theorem states that if L/K is a cyclic extension of number fields, then if a nonzero element of K is a local norm everywhere, then it is a global norm. Here to be a global norm means to be an element k of K such that there is an element l of L with 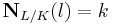$\mathbf{N}_{L/K}(l) = k$ ; in other words k is a relative norm of some element of the extension field L. To be a local norm means that for some prime p of K and some prime P of L lying over K, then k is a norm from L_P; here the "prime" p can be an archimedean valuation, and the theorem is a statement about completions in all valuations, archimedean and non-archimedean.

The theorem is no longer true in general if the extension is abelian but not cyclic. A counter-example is given by the field 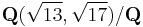${\mathbf Q}(\sqrt{13},\sqrt{17})/{\mathbf Q}$ where every rational square is a local norm everywhere but 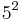$5^2$ is not a global norm.

This is an example of a theorem stating a local-global principle, and is due to Helmut Hasse.

References

H. Hasse, "A history of class field theory", in J.W.S. Cassels and A. Frohlich (edd), Algebraic number theory, Academic Press, 1973. Chap.XI.
G. Janusz, Algebraic number fields, Academic Press, 1973. Theorem V.4.5, p.156